Research Interest

My primary research interest is in the field of active matter. Migration of cells on a substrate, swimming of microbes in solution to movements of large folks of animals are few of the numerous examples, found in nature. Understanding and reciprocating their individual and collective movements, their collective behaviors have become a topic of involved investigation from both basic and applied science. Moreover, recent improvement in numerical techniques, advancement in experiments and in vitro realizations of synthetic motile units present an unique opportunity to verify established particulate, kinetic, stochastic and hydrodynamic theories and inter-relations. Numerous dynamical phases, nonlinear steady states, their transitions, counterintuitive effets of fluctuations, collective responses due to emergent, non-conserved and broken symmetry modes in those out of equilibrium statistical physics highlight the relevance of those active systems in improving underestanding and probable applications in future technologies.

Published Works

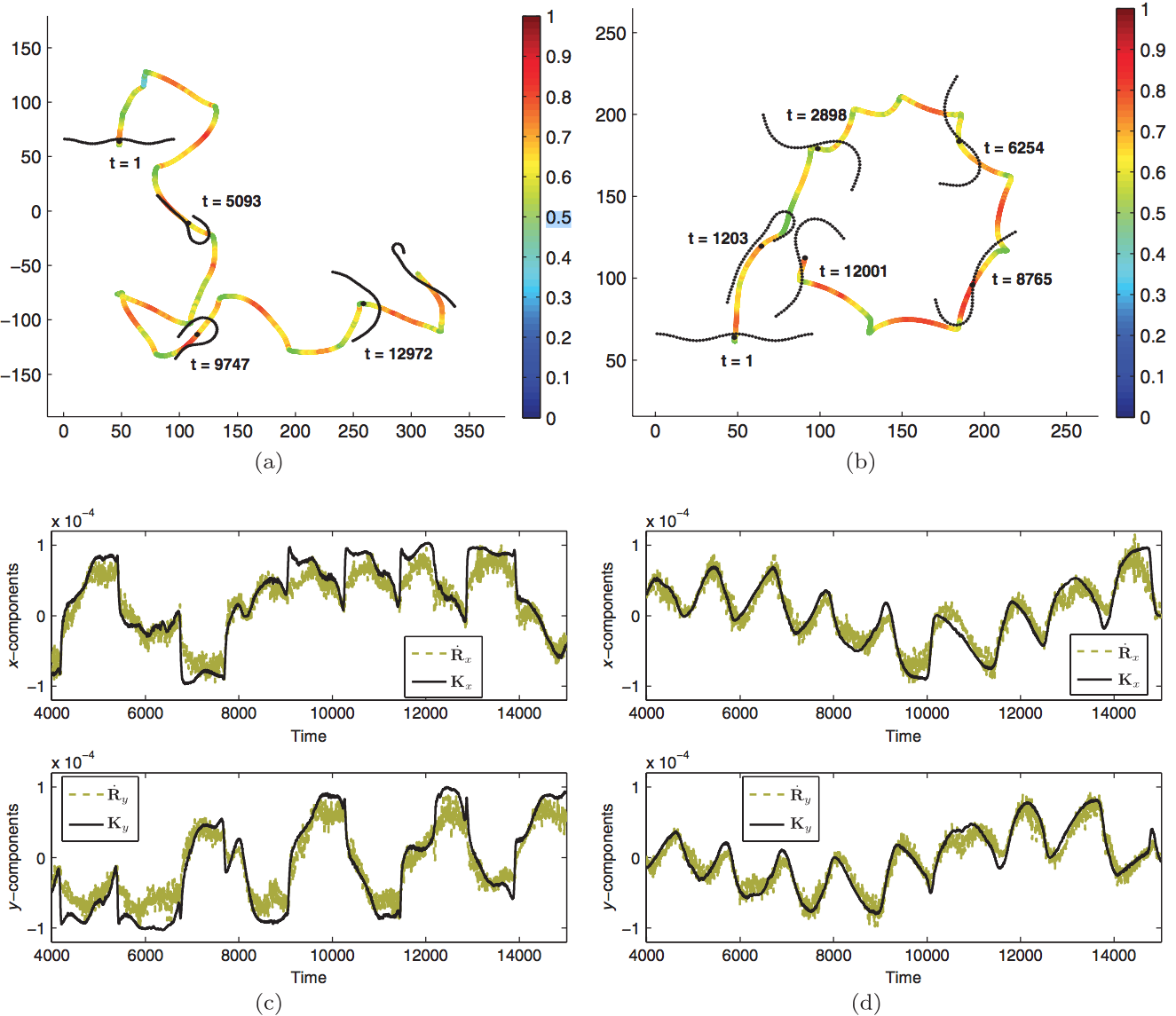
Brownian microhydrodynamics of active filaments.

Soft Matter, RSC Publication (2015) or preprint version. Cover image Soft Matter, RSC Publication (2015).

Slender bodies capable of spontaneous motion in the absence of external actuation in an otherwise quiescent fluid are common in biological, physical and technological contexts. The interplay between the spontaneous fluid flow, Brownian motion, and the elasticity of the body presents a challenging fluid-structure interaction problem. Here, we model this problem by approximating the slender body as an elastic filament that can impose non-equilibrium velocities or stresses at the fluid-structure interface. We derive equations of motion for such an active filament by enforcing momentum conservation in the fluid-structure interaction and assuming slow viscous flow in the fluid. The fluid-structure interaction is obtained, to any desired degree of accuracy, through the solution of an integral equation. A simplified form of the equations of motion, which allows for efficient numerical solutions, is obtained by applying the Kirkwood-Riseman superposition approximation to the integral equation. We use this form of equation of motion to study dynamical steady states in free and hinged minimally active filaments. Our model provides the foundation to study collective phenomena in momentum-conserving, Brownian, active filament suspensions.

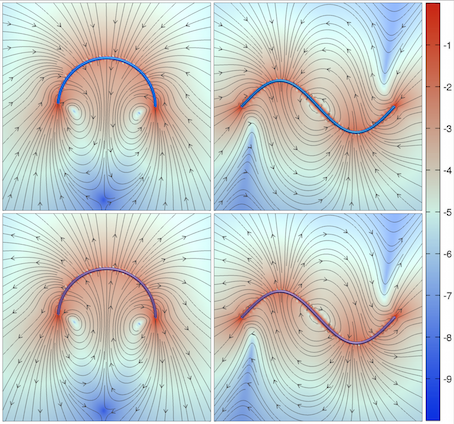
Hydrodynamic Instabilities Provide a Generic Route to Spontaneous Biomimetic Oscillations in Active Filaments.

Scientific Reports, Nature (2013) or preprint version. Non-equilibrium processes which convert chemical energy into mechanical motion enable the motility of organisms. Bundles of inextensible filaments driven by energy transduction of molecular motors form essential components of micron-scale motility engines like cilia and flagella. The mimicry of cilia-like motion in recent experiments on synthetic active filaments supports the idea that generic physical mechanisms may be sufficient to generate such motion. Here we show, theoretically, that the competition between the destabilising effect of hydrodynamic interactions induced by force-free and torque-free chemomechanically active flows, and the stabilising effect of nonlinear elasticity, provides a generic route to spontaneous oscillations in active filaments. These oscillations, reminiscent of prokaryotic and eukaryotic flagellar motion, are obtained without having to invoke structural complexity or biochemical regulation. This minimality implies that biomimetic oscillations, previously observed only in complex bundles of active filaments, can be replicated in simple chains of generic chemomechanically active beads.

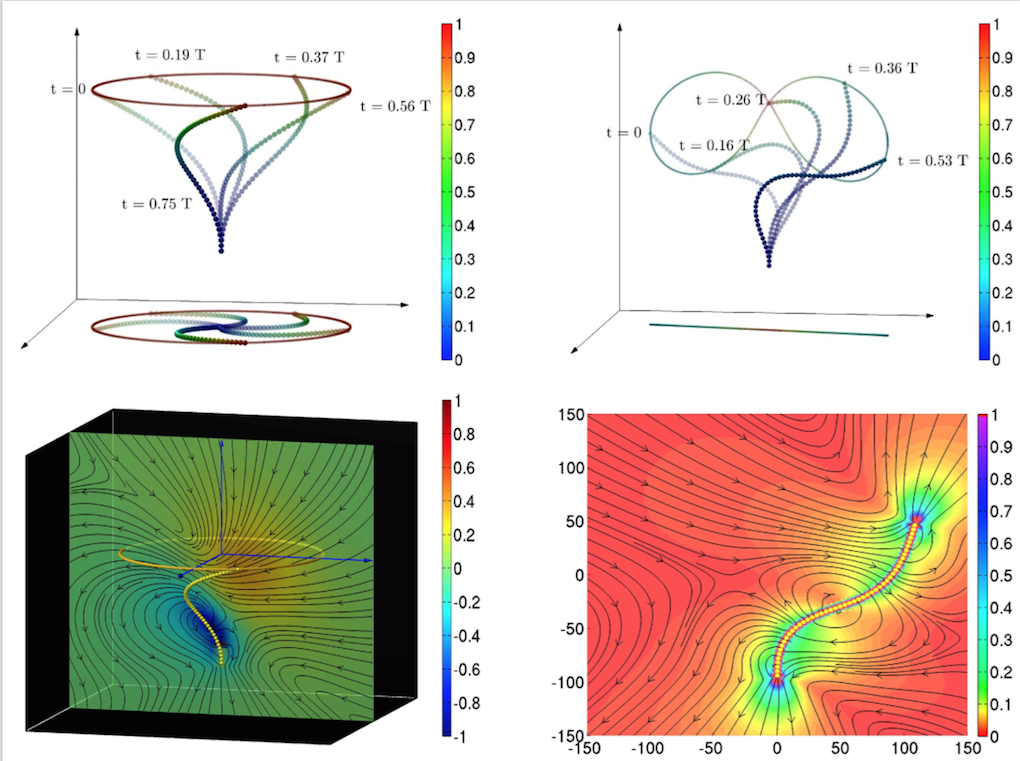
Autonomous Motility of Active Filaments due to Spontaneous Symmetry Breaking.

Physical Review Letters, 109, 158302 (2012) or preprint version.

We simulate the nonlocal Stokesian hydrodynamics of an elastic filament which is active due a permanent distribution of stresslets along its contour. A bending instability of an initially straight filament spontaneously breaks flow symmetry and leads to autonomous filament motion which, depending on conformational symmetry, can be translational or rotational. At high ratios of activity to elasticity, the linear instability develops into nonlinear fluctuating states with large amplitude deformations. The dynamics of these states can be qualitatively understood as a superposition of translational and rotational motion associated with filament conformational modes of opposite symmetry. Our results can be tested in molecular-motor filament mixtures, synthetic chains of autocatalytic particles, or other linearly connected systems where chemical energy is converted to mechanical energy in a fluid environment.